Dr. Samo Sali
salilab.org
My specialty is the woodcutting process and the acoustics. The object of my research is the classical guitar. I have finished my Doctor's degree with title: "ALGORITHM FOR OPTIMIZATION OF THE ACOUSTIC RESPONSE OF WOOD". The thesis research includes results that may be interesting to guitarmakers, both with small and large scale production.
Abstract of current research:
Constructing a guitar by copying only the dimensions, design features, and wood species of a high quality guitar does not ensure high sound quality. This is due primarily to non-homogeneity and anisotropy of wood. I proposed a systematic approach to improving the guitar sound during the production process. This is achieved by additional trimming of the braces' height, after the guitar is already assembled. This procedure changes the modal behavior of the parts with braces, which results in a better sound when certain rules are followed (see below).
To find a way for sound improvement with additional cutting of wooden braces on the resonant board, it was necessary to define objectively the quality of guitar sound. Experiments with some high and low quality classical guitars showed significant differences in the amplitude frequency spectra of the corresponding tones. The timbre of good tones consists of stronger consonant (pleasant) and weaker dissonant (unpleasant) intervals (intervals consist of two frequency components). We named this empirical criterion of sound quality 'rule of consonance-dissonance' (RC-D). RC-D was interpreted in physical and musical terms; it is also described in the mathematical form.
After experimenting with test guitars and many resonant boards with braces, it was found that there is a possibility for controlled sound improvement. When the sound was not as good as it could be, the lowering of one particular brace for certain amount resulted in improved sound. The rules for sound improvement of sanded and planed resonant boards are different.
The Influence of Different Machining process on the Acoustic Properties of Wooden Resonant Board
How important is the machining process for mechanical (acoustic) properties of the resonant board for the classical guitar?
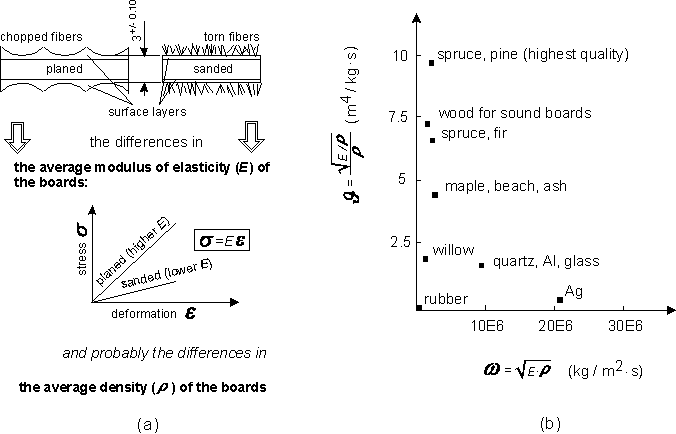
The influence of the machining wooden resonant boards for guitars on the theoretical acoustic properties of this instrument has been studied. Square-shaped spruce boards (Picea abies Karst.) were selected to represent a typical portion of the guitar resonant board. Three different machining processes were used to prepare the test specimens: planing, sanding and milling. Vibration of the specimens was initiated by impacting them with a small wooden ball. The resulting oscillations, measured by an accelerometer mounted on the board, were processed by a frequency analyser. The measured response of the differently machined boards was analysed statistically in terms of amplitude, damping and power spectrum, in order to distinguish between the different acoustic properties of the boards. For the given material, board shape, and board fixture, it was found that the selected type of machining had a strong effect on the vibrational, and thus acoustic, properties of the tested boards, as illustrated by the figures below.
There is a significant difference, after the ball's impact, between the acceleration of a planed wooden plate and a sanded wooden plate. This difference is significant at the statistical rejection level better than 5%. The acceleration corresponds to the fundamental frequency:
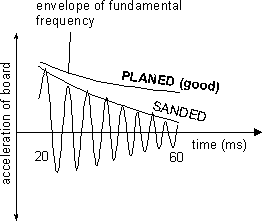
There is also a significant difference among the planed, sanded, and milled wooden plates in terms of the strongest components of the acceleration power spectrum:
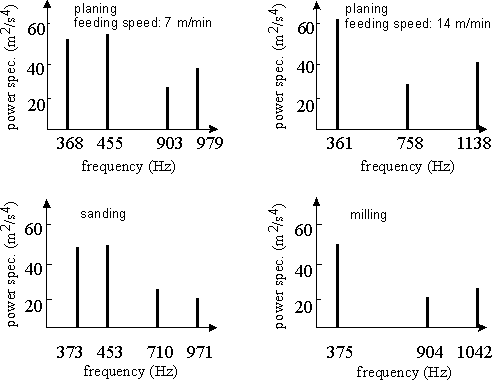
Conclusions:
1. All three tested cutting processes and their technological parameters were suitable for generating a good surface quality of the specimens made from two types of wood. In one type of tested wood (spruce, seasoned for 5 years) the roles of feeding speed and depth of cut in planing were estimated. The comparison of planing, sanding and milling was performed with specimens made from another spruce, which was seasoned for 30 years. Sometimes acceleration of differently machined specimens differed significantly, which was proved with statistical tests.
2. The cutting process affects the average modulus of elasticity and probably also the average density of wooden boards.
3. The significant correlation between the cutting process and the theoretical acoustic properties of a wooden resonant board is established and explained by the modulus of elasticity and density.
4. Experiments with both types of wood showed superiority of planing with low feeding speed and small depth of cut.
No implications for guitarmaking could as yet be made. Perhaps the observed correlation is not even important for making resonant boards of real guitars. Only future experiments can help us understand the interplay between the cutting process and the acoustic properties of the resultant resonant board. However, the current results and experimental set-up provide a good starting point to address this larger question.
Sound Improvement Through Brace Trimming
It was hypothesised that changing the height of braces would result in a different sound. The aim was to find such changes in the brace height that result in an improved sound. All experiments were done with only one test guitar. The variable was the front resonant board with braces. Other braces were considered as part of the resonant board and were also changed when the board was changed. All braces were glued with a glue that was not resistant to heat. Thus, the braces could be removed with a hair dryer. The inner side of the front resonant board was made accessible by reversibly screwing the back board on the rim of the resonance box. The front boards were glued on the rim. The trimming of brace heights involved three phases, ungluing, planing, and gluing. All braces and resonant boards were made of spruce (Picea abies Karst.): At 10% moisture content, the density was 451 kg/m**3 (standard deviation: 7 kg/m**3). The sketch of the resonant board:
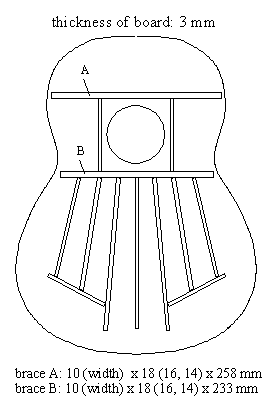
Sanded Resonant Board - Sound Quality Measurements
The average sound quality of the tones "F", "B", and "g" is denoted as Q_m:
Q_m = (Q_m("F") + Q_m("B") + Q_m("g")) / 3The quality of the three tones is derived from the rule of consonance-dissonance.
The following four figures show the positive and negative effect of lowering of brace B for 4 millimeters.
Positive effect of trimming when brace A is held fixed: (a) Change in the quality of the three tones from before (1st set of 3 bars) to after (2nd set of 3 bars) trimming of brace B; (b) Increase of the average tone quality from before (1st bar) to after (2nd bar) trimming of brace B:
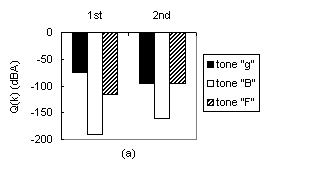
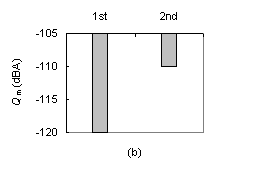
An increase in Q_m was mainly a consequence of improvement in tones "F" and "B".
The quality of tone "g" either increased, decreased or remained unchanged.
Negative effect of trimming when brace A is held fixed: (a) Change in the quality of the three tones from before (1st set of 3 bars) to after (2nd set of 3 bars) trimming of brace B; (b) Increase of the average tone quality from before (1st bar) to after (2nd bar) trimming of brace B:
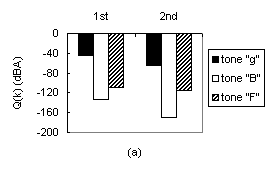
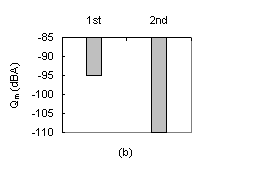
Planed Resonant Boards - Sound Quality Measurements
Exactly the same experiments as described above for the single test guitar were also performed with four planed resonant boards, with dimensions and shapes equal to those of sanded boards. In contrast to the sanded boards, however, trimming of the brace B never improved the average sound quality of the three tones, even when the initial sound quality was bad. After the trimming, the sound quality remained equal or became even worse. A schematic presentation of the comparison of sanded and planed resonant boards (tops) is shown in the following figure:
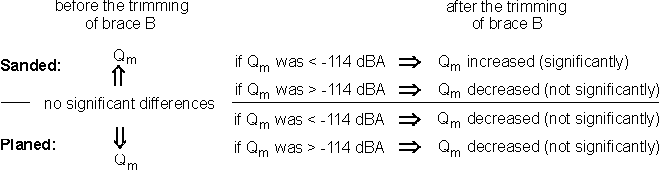
Conclusions
Our criterion for determining the quality of the guitar sound is a result of objective sound measurements and analysis of bad and good classical guitars. The criterion, the rule of consonance-dissonance, was expressed in a mathematical form and interpreted in terms of the physical and musical theory. The essential difference between the bad and good timbre of a guitar tone is in the relative contributions of the consonant and dissonant intervals in the frequency spectrum of the tone.
We proposed and tested a procedure for improving sound quality of the guitar sound; it is based on the assumption that only three tones are enough to describe the guitar's register of tones. According to this procedure, the improvement can generally be achieved by trimming of a certain brace on the front resonant board. In order to refine this procedure, it will be necessary to perform additional experiments exploring various variables, such as the test guitar, resonant boards, braces, wood, etc. Planed boards behaved differently from sanded boards, although their sound quality was similar. It is certain that the cutting process strongly influences the acoustic properties of a wooden plate. This suggests that a comprehensive analysis of acoustic properties of an instrument must include the cutting process as a variable, not a constant. The most probable reason for the different behavior of the differently machined boards is to be sought in the differences in their surface layers. Considering that the thickness of tested boards was only 3 ±0.10 mm, it was clear that the shape of the thin surface layer was important. It is well known that the surfaces of sanded and planed boards are different. Sanded boards have torn fibers whereas planed boards have chopped fibers. Tearing of fibers damages the integrity of the surface much more than chopping. The different shape of surface layers results in either or both of the following consequences from the following figure (a):
and high damping due to sound radiation
are desirable. From the above figure we can see that the ratio
is most advantageous (high) for planed boards and bad (low) for sanded boards. This is reasonable because the planed boards have a surface with smooth chopped fibers that have a higher strength (higher E) in comparison to sanded boards. It is, however, more difficult to discuss the effect of density on the acoustic properties because we do not know the differences in the density of surface layers of the board. For a thorough analysis of the role of surface layers density we would need to know the exact cutting forces on the board, which is impossible for sanding.
Essential Differences Between Good and Bad Guitar Sound
(rule of consonance-dissonance)
The string exciter assured that bad and good guitars were tested under equal conditions. The sound was measured with non-directional condenser microphone, 180 mm from the front resonant board. The quality of guitar's sound was defined on the basis of three tones:
- "F" - 87.3 Hz (6th string)
- "B" - 123.5 Hz (5th string)
- "g" - 196.0 Hz (3rd string
Let' s see the difference between tones "F" at 0,2 s after string excitement of really bad and really good guitar (A-weighted spectrum, reference pressure = 0,00002 Pa, frequency resolution = 86,13 Hz):
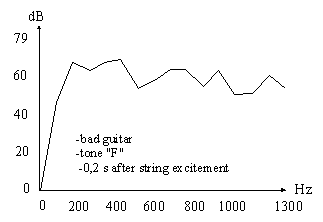
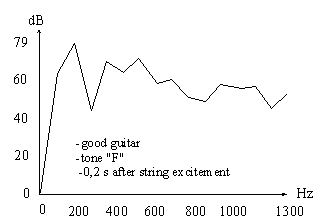
Both spectra have characteristically guitar sound, but what a difference between them!
A simultaneous combination of two tones, which is pleasing to the ear, is termed consonant. When a combination of tones is not pleasing to the ear, the sound is termed dissonant. The consonant combinations of tones have the ratio of fundamental frequencies of two integer numbers none of which is large; for example, 2:1, 3:2, 5:3, 4:3, etc. (H.F. Olson: Music, Physics and Engineering).
The combination of two tones can be seen as an interval of the fundamental frequencies of the tones. Similarly the spectrum of any tone can be seen as a host of intervals where each interval consists of two frequency lines. This host of intervals includes both consonant and dissonant intervals. When the difference in Hz between a certain frequency line and fundamental frequency of some scale tone (scale with tone a1=440 Hz was used) is less than 1%, the frequency line can be considered as a fictitious tone and gets the name of the scale tone. For the tone "F" (recorded 0.2 s after string excitation), the fictitious tones with sample spectra of good and bad tones are shown in the following figure. The names of the fictitious tones are in parentheses under the numbers of the corresponding frequency lines (components). Note that A-weighted sound pressure level (SPL) of some frequency lines (components) differ by more than 10 dBA.
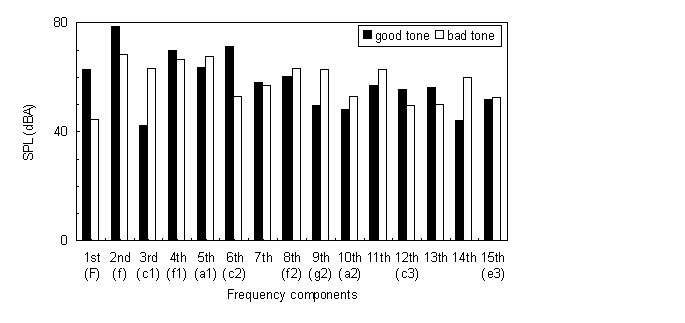
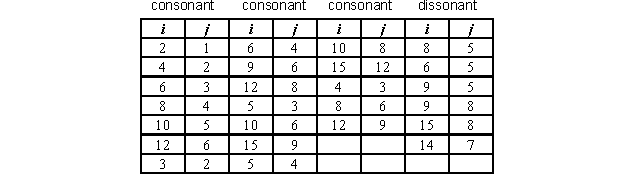
The 11th and 13th frequency lines are excluded from the analysis of intervals, because their position does not match a fundamental frequency of any scale tone. The 7th and 14th frequency lines form a consonant interval inside a tone spectrum, but they are considered as a dissonant interval, because the difference between them and the fundamental frequencies of any scale tone is bigger than 1%. Out of the 105 (15x14/2) intervals for the first 15 frequency lines, we considered 25 intervals, 19 of which are consonant. The SPL of interval L_ij(k), consisting of frequency lines i and j, is:
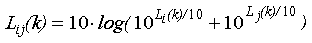
where L_i(k) and L_j(k) are the A-weighted SPL of the first and the second frequency line of the interval ij, respectively, and k indicates one of the tones "F", "B" or "g". The 25 considered combinations of ij are shown in the following table:
The difference of L_ij(k) for the good and bad tones of the same pitch gives the parameter dL_ij(k):
dL_ij(k) = L_ij(k: good guitar) - L_ij (k: bad guitar)
The following terms can now be defined:
The consonance (C_G(k)) of a good tone k relative to a bad tone k, is defined as the sum of the consonant dLij(k) that are larger than 0.
The dissonance (D_G(k)) of a good tone k relative to a bad tone k, is defined as the sum of the dissonant dLij(k) that are larger than 0.
The consonance (C_B(k)) of a bad tone k relative to a good tone k, is defined as the sum of the consonant dLij(k) that are smaller than 0.
The dissonance (D_B(k)) of a bad tone k relative to a good tone k, is defined as the sum of the dissonant dLij(k) that are smaller than 0.
Since each tone of bad and good guitars (4 bad and 4 good guitars were tested) was recorded in three different periods after string excitation, 144 (4 guitars x 4 guitars x 3 periods x 3 tones) comparisons between good and bad tones were made. For each comparison of good and bad tone, recorded after the same time after string excitation, the following expression is significant:
(C_G(k)+C _B(k))>2(D_G(k)+D_B(k))
This expression is named the rule of consonance-dissonance (RC-D) and means a criterion for distinguishing the bad guitar tone from good one.
When two tones of the same pitch are recorded under equal conditions, the quality of the bad tone in comparison to the good tone can be defined as:
Q(k) = D_G(k) + D_B(k) - C_B(k) - C_G(k)
Larger Q(k) indicates a better quality of the bad (i.e., tested) tone in comparison to the good tone.
Material herein added and updated constantly; presented for inspirational and educational purposes per Fair Use.
Last modified 16 Feb 2024
